Byers, J.A. 1996. Temporal clumping of bark beetle arrival at pheromone traps: Modeling anemotaxis in chaotic plumes. Journal of Chemical Ecology. 22:2133-2155. pdf

JOHN A. BYERS

Department of Plant Protection, Chemical Ecology
Swedish University of Agricultural Sciences
S-230 53 Alnarp, Sweden
 Present address:


Portable fraction collector and pipe trap for catching bark beetles.
Abstract--The sequence of arrival of the bark beetles Ips typographus and Pityogenes chalcographus (Coleoptera: Scolytidae) at traps baited with their synthetic pheromones was monitored with a portable fraction collector. Histograms of the natural arrival patterns of both species were non-random and clumped at shorter time scales (1, 2, 4, 5 or 6 minute cells) but appeared random at larger time scales (10, 20 or 30 min). Monte Carlo generation of similar histograms showed them to be random at all of these time scales. A stochastic computer model could graphically simulate insect orientation to odor sources based on present theories of odor-modulated anemotaxis and casting. Although this model was used throughout since it assumes only that insects cast perpendicular to the current wind direction, a second model could slightly improve orientation success. However, the second model requires that the insect remember its ground path (upwind) prior to losing the plume (after an abrupt wind direction change). The effects of casting and flight parameters on orientation success and randomness of arrival sequence within various plumes were determined by simulation. Similarly, the effects of random-walks in plume direction, plume width, and wind speed were explored. The results showed that dynamic random variations in plume direction and especially wind speed could cause an otherwise random arrival sequence (e.g., under constant wind) to become clumped and non-random. Therefore, the clumped arrival patterns of bark beetles and other insects, including Spodoptera litura (data from Nakamura and Kawasaki, 1984), at pheromone sources could result from random-walk fluctuations in wind speed and wind direction.

Key Words--Orientation, attraction, odor-modulated anemotaxis, pheromone plumes, casting, simulation models, Coleoptera, Scolytidae, Lepidoptera
Running Title: SIMULATED ORIENTATION IN PHEROMONE PLUMES

INTRODUCTION

In 1984, spruce bark beetles, Ips typographus (Coleoptera: Scolytidae), were collected by a fraction collector as they arrived at a trap baited with synthetic pheromone (Byers and Löfqvist, 1989). It appeared that the arrival of these beetles at the trap occurred in groups and not uniformly random during an hour with relatively constant temperature. I questioned this, however, because Ripley (1981) stated that a random pattern, such as a "Poisson forest" or the stars in the sky, appears to a casual observer as a non-random pattern of groups (e.g. the mythological constellations). On the other hand, it is reasonable to suppose that non-random patterns of arrival could result from difficulties of insects to orient in pheromone plumes under certain meteorological conditions. Thus, the first objective here was to determine whether individuals of two species of bark beetle arrive at pheromone-baited traps in a non-random, clumped sequence.

The optomotor anemotaxis mechanism for orientating to pheromone sources proposed for insects, especially moths (Kennedy, 1939, 1983; David et al., 1982; Baker and Haynes, 1987; Baker, 1989), probably also functions in bark beetles (Choudhury and Kennedy, 1980). In this theory, an insect attempts to fly directly upwind when in contact with a packet of pheromone-laden air of the plume, but casts (flying back and forth perpendicular to the wind) when contact is lost. In contrast to walking insects, insects that are flying probably can not use mechanoreceptors to sense the wind direction. However, flying insects can perceive wind direction by observing the ground below: in head-on wind, the ground moves directly underneath during flight. If the visual ground field moves from right to left somewhat, for example, then wind is coming from the left. The insect thus turns to the left to minimize the transverse ground shift and keep the ground moving directly underneath in order to head upwind toward the pheromone source. However, it is not known if all insect species use the same orientation mechanisms when flying within or on the edge of a pheromone plume.

The seminal paper of David et al. (1982) advanced our thinking about how flying insects reach a pheromone source in the field. Their theory, called "odor-modulated anemotaxis", asserts that optomotor anemotaxis and casting are sufficient to cause orientation to the odor source. They showed that wind direction may change rapidly causing a "snaking" of the plume, much as one might spray water from a hose. This occurs because the volume of air passing the odor source continues in a straight line downwind - and thus any insects encountering this volume will experience a wind direction flow that is directly opposite the direction to the source. They maintain that all the insect has to do is fly upwind, using optomotor anemotaxis when detecting pheromone, and cast when not detecting pheromone in the expectation of reentering the plume.

Central to our understanding of orientation is the structure of the pheromone plume - in which our knowledge also has gone through an evolution. Plumes were visualized earlier as time-averaged Gaussian plumes extending up to several kilometers (Bossert and Wilson, 1963). Other Gaussian plume models have been proposed (Fares et al., 1980) but these and others did not reliably predict when gypsy moth wing-fanning would occur in relation to the mean wind direction (Elkinton et al., 1984). Since then the idea of a filamentous and "snaking" plume has become the paradigm (Murlis and Jones, 1981; David et al., 1982; Elkinton and Cardé, 1984). The idea of the "active zone" (Bossert and Wilson, 1963) or "active space" (Nakamura and Kawasaki, 1977, 1984; Baker and Roelofs, 1981) is also central to our concept of a plume. Within the active space the concentration of pheromone molecules is sufficient to elicit a behavioral response in an insect and this is the area that we spatially visualize as the plume.

My second objective was to make a computer model to simulate the odor-modulated anemotaxis and casting mechanisms associated with a plume in order to understand better how flying insects find a pheromone source. Using Monte Carlo randomization methods, several plume- and insect-related parameters were simulated over wide ranges (overlapping most natural conditions) to help understand their individual effects on insect attraction to pheromone. The third objective was to discover whether certain meteorological parameters that varied at random in the simulation model could frequently produce non-random, clumped arrival patterns similar to those observed in nature.

METHODS AND MATERIALS

Successive catches of bark beetles attracted to pheromone components. A portable fraction collector similar to that used earlier (Byers, 1983), but with a crystal-controlled timer (Byers unpublished), was used to sequentially collect flying bark beetles in 1- or 2-min periods during their attraction to pheromone baits. Ips typographus were collected this way during one to several hours in a Norway spruce forest clearcut located in Grib Skov, 30 km northwest of Copenhagen, Denmark (29 May and 5 June 1984), as they oriented to drain pipe traps (with funnel) releasing 2-methyl-3-buten-2-ol (50 mg/day) and (1S,4S,5S)-cis-verbenol (1 mg/day) (Bakke et al., 1977; Bakke et al., 1983; Byers et al., 1988). The fraction collector with only a 30 cm diameter funnel was used to simultaneously collect I. typographus and Pityogenes chalcographus attracted by pheromone components of both species in another Norway spruce forest clearcut in Grib Skov (16-17 June 1987). P. chalcographus was attracted by baits releasing chalcogran (46:54 E:Z, 98% pure from W. Francke, Univ. of Hamburg, Germany) released at 1 mg/day and methyl (E,Z)-2,4-decadienoate (99.5% pure, Cyanamid Agrar) at 0.1 mg/day (Francke et al., 1977; Byers et al., 1988, 1990). During collections, the pipe trap+funnel or funnel was strongly tapped every 10-30 seconds to insure that all beetles were immediately collected after landing. Sex and numbers of beetles collected in the periods were determined in the laboratory.

Simulation of insect movement during orientation and casting in pheromone plumes under windy conditions. The simulation model (Figure 1) requires 30 input parameters (in units of m, s, degrees, or as indicated). Twenty of these parameters can be varied systematically over a number of simulations. The parameters and their usual values, unless varied during simulation, were: (1) number of simulations per step variable, 8 or 16; (2) number of insects, 50; (3) x-axis, 216; (4) y-axis, 162; (5) plume length, 100; (6) flight speed in plume, 2; (7) cast proportion, 0.5; (8) number of castings, 2; (9) checks per cast, 20; (10) flight speed outside plume, 2; (11) trap radius, 0.25; (12) minimum wind speed, 0 or 1; (13) maximum wind speed, 1 or 2.5; (14) minimum wind speed enabling anemotaxis, 0.2; (15) maximum wind speed changes/min, 0, 1, 10 or 30; (16) maximum wind speed change per change, 0 or 0.5; (17) angle of maximum turn in plume, 20; (18) angle of maximum turn outside plume, 20; (19) probability of orienting during move when in plume, 1; (20) maximum plume angle, 90 or 160; (21) minimum plume angle, 20 or 90; (22) maximum plume angle changes/min, 0 or 10; (23) maximum plume angle change per change, 0 or 5; (24) maximum plume width angle, 10; (25) minimum plume width angle, 10; (26) maximum plume width angle changes/min, 0 or 5; (27) maximum plume width angle change per change, 0 or 5; (28) number moves per time period, 300; (29) total time periods, 12; (30) random seed number, varied.


Fig. 1. Flow diagram of graphical computer model for orientation of insects toward pheromone-baited traps while flying in changing wind and plume structure.
The complexity of the model can be reduced by choosing parameters that are realistic, such as X- and Y-axes, plume length, insect number per area, flight speeds, and turning angles (usually < = 20 degrees). Variations in other parameters often have little effect or may be optimized, such as cast proportion, number of casts, and number of checks per cast. Many parameters can be ignored by making them equal zero. Other effects can be held constant by setting two parameters equal, for example, minimum and maximum wind speeds both set to 1 m/s.

The general algorithms for simulation of insect movement and catch by traps have been described in Byers (1991, 1993). A plume in the models is defined geometrically as a "pie-slice" of a circle with width equal to the arc in degrees and length equal to the radius (Sabelis and Schippers, 1984). Insects not in contact with the plume take steps in a forward direction with possible random deviations up to an angle of maximum turn (either right or left at random). Moves are based on either of two speeds (or distances covered in one second) when either inside or outside the plume. However, insects can have less ground speed when casting or when countered by the wind. The ground path of an insect is determined by first calculating the insect vector using polar coordinates of insect flight speed and former direction (or upwind direction if in the plume) plus the random angle of turn, and then adding the wind vector, based on the polar coordinates of wind direction and speed. Insects that land in or cross the trap during a move are caught (Byers, 1991) and recorded for the time period. During a move, any insects that are caught or leave the arena are removed (Figure 1). After all insects have moved a step, the number of insects remaining outside the plume that are not casting are counted. If this number is less than the expected number based on the initial density (minus the plume area) then enough insects are added at the arena's periphery (in proportion to the dimensions) to attain the desired density (Figure 1). This insures that a relatively constant density of insects surrounds the plume under any conditions.

Modelled insects cast after they step out of a plume, through a plume, or when the plume moves away between insect moves (Figure 1). The algorithm for determining whether an insect is within the plume is based on whether the insect's angle to the source is within the plume angles and that the insect is closer to the source than the plume length. Near the source as the plume narrows, it is possible for insects to "step over the plume" so a second algorithm is used to determine if the insect's move segment intersects either plume segment (Byers, 1992). When an insect either steps over the plume or leaves the plume, it does not begin casting until the next move, whereupon it turns perpendicular to the wind direction by turning either right or left at random.

The distance of a cast, defined as the maximum length of a perpendicular excursion, can be specified as any proportion P of the distance covered in one second while in the plume (flight speed within the plume). The insect takes one move to travel the cast distance and one move to return to the starting point. The insect checks to see whether it is in the plume at several points spaced equidistantly along the cast path. The number of checks can be varied but was usually held constant at 20 in the simulations here. If the insect encounters the plume while casting at any of the check points, it stops at this position and on the next move begins to fly upwind again (Figure 1).

Assuming the plume is not found during a cast and return, the casting oscillation continues until the insect takes a cast in the direction opposite the initial one (a third move) and then returns to the start on the fourth move. More than one casting oscillation can be specified during a bout of casting (in the simulations the default was 2 oscillations). After casting is completed without success, the insect wanders away to possibly blunder into the plume nearby. This casting algorithm causes insects to orient reliably to the pheromone source except when the plume is very narrow (a few degrees) or very wide. The maximum width of the plume (in degrees) that should allow reliable plume following is calculated from the following equation:

where S is the flight speed (m/s) within the plume, W is the wind speed (m/s), P is the cast proportion (± 1), and a is the angle of maximum turn within the plume (in radians). The largest a possible for casting to function reliably is limited by the cast proportion according to:

The a used in simulations should be less than amax since this angle assumes the most narrow plume possible. The arcsin transformation (2), uses the ATN (arctan) function of BASIC and should also be used with equation (1).

To understand the effects of certain parameters on catch in simulations, several combinations of parameters were held constant while the magnitude of one parameter was increased stepwise, with 8 or 16 replicates per step and each replicate had 12 time periods consisting of 5 minutes (300 moves). Attempts were made to simulate the frequency distributions of natural catches by allowing several meteorological parameters to vary at random during simulations. These were wind speed, plume direction angle (wind direction), and plume width. All three variables have two components which can also be varied at random, namely, probable number of changes per minute and maximum random change at each change. The probable number of specified changes, e.g., 10 changes in wind speed per minute, is determined at each move (equal to one second) by whether the random number generated by computer (an 8-digit number < 1) is less than 10/60.

The arrival patterns of bark beetles were analyzed for randomness over different time periods by making histograms of the catches using various cell widths (1 to 30 min). These histograms were compared to average expected catches based on the total catch divided by the number of histogram cells using chi-square analysis. To check the method, histograms of the same number of cells and total catch were generated by Monte Carlo methods and compared similarly. The catches in the computer simulations were also grouped in 5-min periods and analyzed by chi-square whereupon exact P values were calculated and averaged for graphical and statistical analyses. Points with bars in the figures represent upper and lower S.E.X. from 8 to 16 simulation runs (however, some graphs have no bars to reduce complexity). Curves were fitted to the data with the following priority of methods: linear and non-linear regression, combinations of these, equation fitting by eye, moving-average, and connection of points.


RESULTS

Successive catches of bark beetles attracted to pheromone components. A total of 108 (27.8 % males) I. typographus were collected in 2-min periods over 3.5 hours beginning at 14:30, 29 May 1984. The pattern of arrival, as shown in a histogram of 5-min periods (Figure 2) summarizing the actual counts (dots), was significantly different from an expected distribution based on a uniform random arrival (P = 0.028, chi-square). A Monte Carlo generated histogram of the same total count shown for comparison was not different, as expected, from a uniform random arrival (P = 0.664) nor was an average of ten such distributions (Figure 2).
Fig. 2. Top: histogram of Ips typographus arrival at pheromone-baited traps (5-min periods over 3.5 hours beginning 14:30 on 29 May 1984; actual 2-min catches represented by dots) and Bottom: histogram of Monte Carlo- generated random distributions of the same number of periods and total catch (108). Average P value for 10 generated distributions was 0.56 ± 0.28 (± 95% CL).
When the natural data and the randomly generated patterns were subdivided into cells of different durations (1 to 30 min) and analyzed by chi-square, only the natural data was significantly non-random at 2-, 4- and 5-min periods, while larger lumpings of the data in cells of 10 or more minutes indicated a relatively constant catch during the whole period (Table 1). On 5 June 1984, 62 (16.1% males) I. typographus were caught over an hour period (Table 1) and histograms of cells of 2 to 6 min also were significantly different from random while larger groupings were not (Table 1).

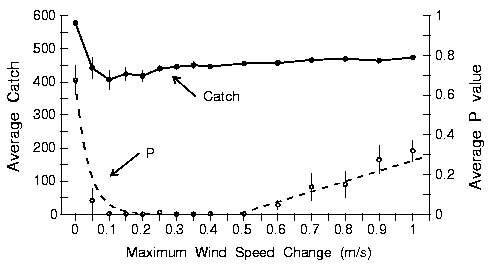
Table 1. Chi-square analysis of bark beetle arrivals at pheromone-baited traps in the field. The arrival patterns were partitioned into various histograms of different cell widths (1 to 30 min) and compared to average expected frequencies based on total catches using chi-square analysis. P values less than 0.05 indicate that a distribution of catch is not uniformly random.
Minutes per Histogram Cell
1 2 4 5 6 10 20 30
Ips typographus
May 29, 1984 (14:30)
df - 104 51 41 34 20 9 6
P value - 0.005 0.004 0.028 0.054 0.326 0.518 0.607
June 5, 1984 (14:30)
df - 29 14 11 9 5 2 1
P value - 0.004 0.002 0.063 0.007 0.310 0.290 0.450
Pityogenes chalcographus
June 16, 1987 (14:30)
df - 19 9 7 5 3 1 -
P value - < 0.001 < 0.001 0.016 0.013 0.141 0.033 -
June 16, 1987 (15:18)
df 19 9 4 3 2 1 - -
P value < 0.001 < 0.001 0.002 < 0.001 0.002 0.003 - -
June 17, 1987 (14:46)
df 19 9 4 3 2 1 - -
P value 0.009 0.134 0.015 0.018 0.068 0.222 - -
June 16, 1987 (15:18) df 19 9 4 3 2 1 - - P value <.001 <.001 .002 <.001 .002 .003 - - June 17, 1987 (14:46) df 19 9 4 3 2 1 - - P value .009 .134 .015 .018 .068 .222 - - Over a 40-min period of 2-min collections, 226 (40.7% males) P. chalcographus were caught and the histogram pattern (Figure 3) was significantly different from an expected distribution of random arrival (P < 0.001). Similar Monte Carlo generated distributions, however, were not different from random as analyzed by chi-square (Figure 3). In two other 40-min periods of 1-min collections, 93 (44.1% males) and 81 (39.5%) P. chalcographus were caught and the histograms were significantly different from expected random arrivals at several different lumpings of the data from 1 to 10 min (Table 1). As expected, similar chi-square analyses of Monte Carlo generated histograms rarely (<= 5% cases) were found to be different from random.

Fig. 3. Top: histogram of Pityogenes chalcographus arrival at pheromone-baited traps (2-min periods over 40 minutes beginning 14:30 on 16 June 1987) and Bottom: histogram of Monte Carlo-generated random distributions of the same number of periods and total catch (226). Average P value for 10 generated distributions was 0.58 ± 0.16 (± 95% CL).
The temperature during the 40-min collection periods varied less than 2o and was generally optimal for flight (21-25o). Winds were measured occasionally with a fan anemometer and varied between 0.8 and 2.3 m/s (average for 20 s). Wind direction was observed with a wind vane to change direction up to 60o within a second or two while generally prevailing in one direction (although direction reversals were observed). It appeared that most beetles arrived during lulls in the wind.

Simulation of insect movement during orientation and casting in pheromone plumes under windy conditions. The computer model shows on screen whether the parameters specified allow simulated insect orientation toward a pheromone source. When the model was tested under constant conditions (parameters as in Figure 4), the effect of enlarging the width of the plume from 0 to 9 degrees caused a cumulative exponential increase in catch (Figure 4).
Fig. 4. Effect of plume width angle on the average catch and the average P value (chi-square analysis of arrival histogram) over an hour of simulated time. Simulations were performed 16 times at each plume width under the following conditions: 216 x 162 m arena; 100 m plume length; 50 insects; 2 m/s flight speed both inside and outside plume; 0.25 m trap radius; 1 m/s constant wind; 20o angle of maximum turn both inside and outside plume; probability of 1 to orient at each step within the plume; 0.5 casting proportion of flight speed within plume; 20 checks per cast; 2 casting oscillations; 90o constant plume direction; plume width angle was varied; constant plume width during a simulation; 300 moves/time period (5-min); and 12 time periods ( total 1 h) per simulation.
Thereafter, an increase in plume width up to about 40o caused a linear increase in catch. In theory, the catch should be linearly proportional to the perimeter length of the plume, i.e., a 90o plume will catch twice as many as a 45o plume of the same radius since the arcs are proportional to the plume angles. However, as seen from equation (1), a plume width of more than 39.53o does not allow reliable casting with the parameters specified in Figure 4 - and thus the catch declined exponentially (Y=ae-bX ) above this angular width (Figure 4). The arrival patterns in the simulations at all plume widths had average P values well above significant levels, indicating that arrival was random as should be expected (Figure 4).

Several parameters involving orientation such as checks per cast, casting oscillations, angle of maximum turn within the plume, and probability of orientation at each step were investigated for their affects on arrival at traps. During a cast an insect must sample the air for pheromone, this can be done only once at the outermost extent of a cast, or many times (equally spaced) along the path of a cast. The orientation success or catch increased with checks per cast approximately in an exponentially-hyperbolic relationship (Y = ae(b/X)) while having no apparent affect on the randomness of arrival (Figure 5A). This relationship was apparent even with 0.5o plume widths, 0.025 m trap radius, and finer 0.1 s insect moves. An increase in the number of casting oscillations had no affect on orientation when plume direction remained constant. When the plume was allowed to shift direction at random (10 times per minute) the orientation success became poorer as the random swing became larger (maximum 1, 5 or 10o). However, orientation success increased as the number of casting oscillations increased - the more so the larger the random swing (Figure 5B).
Fig. 5. (A) Effect of number of casting checks per cast on the average catch and the average P value (chi-square analysis of arrival histogram) over an hour of simulated time. Simulations were performed eight times at each value under the model parameters in Figure 4, except as indicated, and plume width angle was held constant at 5o. (B) Effect of number of casting oscillations on the average catch and the average P value (chi-square analysis of arrival histogram) over an hour of simulated time when the plume direction was allowed to vary in direction at ten directional changes per minute (at random) at a maximum change of 0, 1, 5 or 10 degrees at random. Simulations were performed eight times at each value under the model parameters in Figure 4, except as indicated, and plume direction could range from 20 to 160o while plume width was constant at 10o. (C) Effect of the insect's angle of maximum turn within the plume on the average catch and the average P value (chi-square analysis of arrival histogram) over an hour of simulated time. Simulations were performed eight times at each value under the model parameters in Figure 4, except as indicated, and plume width was constant at 10o.
No effects on the randomness of arrival were found due to the number of casting oscillations.

An increase in the angle of maximum turn from 0 to 27.8o has little affect on orientation success (Figure 5C) and this is expected based on equation (1) for a 10o wide plume. A plume width above 30o does not allow reliable orientation as seen from equation (2). Across the spectrum of possible insect turn angles there was little affect on patterns of arrival since all average P values indicated no differences from random (Figure 5C). The probability of orientation at each step was usually held constant at 1, however, lower probabilities increase the stochasticity and look more realistic on screen. Although no figure is shown, the average catch (Y) increased from 0 to 600 in relation to the square of the probability of orientation at each step (0 < = Po < = 1) according to Y=9.36+563.4Po2 (r2=1, parameters as in Figure 4). Again, average P values indicated random arrivals at all orientation probabilities.

The rate of catch decreased exponentially (best fit was a Taylor exponential: Y=ea-b*(sqr(X)) with an increase in the maximum random change in plume direction "random-walk", when the direction was changed at either 1, 10 or 30 times per minute at random (Figure 6). The catch rate also decreased similarly with an increase in the rate of changes in plume direction (at a maximum random change of 2o per change, figure not shown). Surprisingly, random changes in plume direction (10/min or more) produced a random arrival of insects at the trap over time except when only a few changes per minute occurred (e.g. 1/min, Figure 6).

Fig. 6. Effect of maximum change in a "random-walk" in plume direction (1, 10, and 30 changes per minute at random) on the average catch (top graph) and the average P value (bottom graph) (chi-square analysis of arrival histogram) over an hour of simulated time. Simulations were performed 16 times at each value under the model parameters in Figure 4, except as indicated, and plume direction could range from 20 to 160o while plume width was constant at 10o.


The rate of catch declined as a Taylor exponential (Y=ea+b*sqr(X)) with an increase in plume width changes per minute (each change a maximum of 2o at random) when the plume width could vary between 10-20o or 10-60o (Figure 7). The arrival of insects was different from random when plume widths could vary between 10-60o and the number of width changes were greater than about 10/min, but no effects were observed when plume width was restricted in a more realistic range between 10-20o (Figure 7).


Fig. 7. Effect of number of plume width changes per minute (taken at random) in a "random-walk" at a maximum of 2o per change (at random) on the average catch and the average P value (chi-square analysis of arrival histogram) over an hour of simulated time. Two simulation series were done, one in which the plume width could vary from 10 to 20o and the other with an allowed range from 10 to 60o. Simulations were performed 16 times at each value under the model parameters in Figure 4, except as indicated, and the angle of maximum turn, normally 20o, was reduced to 10o to allow reliable casting on wide plumes.
In preliminary models, attempts to maintain a constant number of insects in the arena were done by replacing any that left the arena or were caught. However, under wind speeds approaching the flight speed, insects accumulated in the plume as they moved slowly toward the source thus depleting the density surrounding the plume. Since there were less insects available to contact the plume, catch rate decreased with time. In reality, in an "ocean" of constant insect density, the same density surrounding the plume should persist at any wind speed. Thus, the model was modified so that any insects that either entered the plume (or were casting), left the arena, or were caught were replaced on the arena's perimeter to obtain the specified density. In this case, at higher wind speeds insects move more slowly toward the source but the accumulation of insects within the plume perfectly compensates so the rate of catch remains constant, until just below the flight speed when orientation is impossible. The wind speed W at which the average insect within the plume cannot move upwind is determined by the following equation:

W = S S cos (b) and b = 0, .0001, ...a (3)
where S is the speed within the plume (e.g., 2 m/s) and a is the maximum angle of turn (e.g., 20o in radians).

Variable winds (random-walks) over a range of 0 to 2.5 m/s had little or no affect on rate of catch but did cause the pattern of arrival to become non-random or clumped. The arrival pattern swiftly became non-random with small increases from 0 to 0.2 m/s in the maximum wind speed change (at random) occurring approximately 30 times per minute (at random) but then gradually became less clumped and more random with further increases above 0.5 m/s in maximum changes (Figure 8).
Fig. 8. Effect of maximum change at random in a "random-walk" in wind speed (about 30 changes per minute at random) on the average catch and the average P value (chi-square analysis of arrival histogram) over an hour of simulated time. Simulations were performed 16 times at each value under the model parameters in Figure 4, except as indicated, and wind speed could range from 0 to 2.5 m/s while plume width was constant at 10o.
The minimum wind speed that enabled anemotaxis was set at 0.2 m/s assuming upwind orientation is not possible without some air movement (Nakamura and Kawasaki, 1984). Below this wind speed insects in contact with pheromone odor continued to move forward with random deviations like those outside the plume.

Wind speed fluctuations that occurred about 30 times per minute at changes of up to 0.5 m/s caused the pattern of arrival (Figure 9) to be non-random (P < 0.002). It appears that catch rate is higher during a lull period following a time with higher winds (Figure 9), although the 5-min rates depend on a complex interaction between wind speed, time, and direction of the speed change.

Fig. 9. Top: Wind speed fluctuations during an hour of simulated time in which wind speed could change on average 30 times per minute at a maximum change of 0.5 m/s at random within a "random-walk" range between 0 and 2.5 m/s. The simulation was performed under the model parameters in Figure 8. Bottom: The corresponding histogram of simulated catch, the arrival sequence was significantly different from an expected frequency by chi- square analysis, P < 0.001.


DISCUSSION

The models here may help us to define, organize, and understand orientation concepts as well as communicate and test that understanding in order to make predictions and comparisons (Worner, 1991). The model has fewer conceptual problems when wind direction, speed, and plume dimensions are held constant at reasonable levels. Objections arise when plume width or direction vary. For example, modelled plumes change direction along their entire length while wind speed and direction changes affect all areas of the arena simultaneously. More realistic "snaking" plumes are the subject of future models. However, the rate of successful orientations within a snaking plume and the swinging plume here may not be significantly different since an insect would experience odor "puffs" of the same periodicity and dimension in both models. Granted, only the snaking plume would allow realistic coordinated movements among insects in the arena, but this seems unimportant to arrival rates.

The model density of 50 beetles in a 216 x 162 m arena was 16% the natural flight density in one spruce clearcut in Denmark (Byers et al., 1989), but of course natural densities must vary greatly. In any case, the relationships and randomness of arrival patterns found here do not depend on insect density. The trap radius of 0.25 m used in the model is larger than most tree trunks, but probably smaller than the visual attraction radius of many bark beetles to trees under colonization (Tilden et al., 1983; Lindgren et al., 1983). Again, this is not important to the general relationships and temporal arrival patterns but only in regard to the absolute catches.

In all simulation series, a period of time to reach equilibrium conditions was allowed before beginning to collect arrival data. Further, in a simulation series each simulation served as the equilibrium period for the next simulation, i.e. all subsequent simulations used the same insects and plume dimensions that existed at the end of the preceding simulation (Figure 1). Attaining equilibrium was especially important at wind speeds approaching the flight speed where many insects, sometimes thousands, could accumulate within the plume.

An increase in the magnitude of plume direction change occurring relatively often (10 to 30/min) did not have a significant affect on the randomness of arrival (Figure 6) even though catch decreased with an increase in the magnitude of directional changes. Many changes in plume direction per minute, each of small magnitude, seems realistic, compared to larger directional changes since the entire plume jumps in the model. Conceptually, a large shift in wind direction might be acceptable if it occurred rarely since in this case the plume position is usually stationary. In this case, when the plume took major swings in direction only once per minute on average at random there were more simulations where arrival was not random, increasingly so with larger directional swings (Figure 6). In nature, changes in wind direction might further affect the arrival patterns since the plume could sweep over brood trees or hibernation sites periodically.

Observations of male Grapholita molesta moths flying to a pheromone source in the field under shifting winds convinced Von Keyserlingk (1984) that males losing the plume allowed themselves to drift or be pushed over to the plume's new position by the wind. Baker and Haynes (1987) did not find evidence to support this phenomenon, instead, males upon leaving a plume seemed to "take up an angle approximately 90o across the windline even as the windline was in the process of shifting". In the simulations here, insects that lost the plume after a wind shift begin casting across the windline, and if unsuccessful in finding the plume, they took their first step forward against the new wind direction (model 1, Figure 10). In a second model (model 2, Figure 10), insects reached the odor source more often in variable winds because upon losing the plume they moved forward initially against the previous wind direction (they would have to remember their immediate ground path).

Fig. 10. Effect of maximum change at random in a "random-walk" in plume direction (at 1 or 10 changes per minute at random) on the average catch over an hour of simulated time for model 1 and model 2 insects. Model 1 insects (those used in most simulations) moved forward in the current wind direction after losing the plume during a wind- shift. Model 2 insects moved forward in the former wind direction after losing the plume during a wind-shift (thus they must remember their previous ground path before casting). Simulations otherwise as in Figure 6.
The reason model 2 insects are more successful in reentering the plume is they have a vector (previous wind direction before wind-shift) that adds to the new plume/wind direction vector causing the insects generally to veer toward the new plume position. Whether plume direction changes rapidly enough in nature to afford an adaptive benefit to model 2 insects remains an open question (Figure 10). Which of these two models insects use should be investigated. Namely, do the initial paths taken after casting progress in the former wind direction before wind shifting, or in the new wind direction?

Changes in plume width can be likened to turbulence. Only when the plume was allowed to broaden or narrow over an unrealistically large range (10 to 60o) could changes in width affect the randomness of arrival (Figure 7). This non-random effect was probably due to histograms composed of fewer catches with a narrow plume during one period of time compared to larger catches with a wide plume at another time in the simulation (see Figure 4). At a smaller range of 10-20o, no effect of plume width changes could be found on arrival pattern, indicating that at even more narrow and probably more realistic ranges there also would be no affects on randomness.

Random-walks in wind speed dramatically modified the arrival pattern to become clumped and non-random (Figures 8 and 9). The effects of wind speed fluctuations were most evident when the wind could vary above and below the flight speed. A wind speed of 0.2 m/s was used as the minimum speed necessary for anemotaxis, and corresponds to the finding of Nakamura and Kawasaki (1984) that the moth Spodoptera litura oriented poorly at low wind speeds. However, removal of this parameter from the model had little affect on the randomness of arrival.

Compared to moths, relatively less is known about bark beetle flight orientation to pheromone. In the confines of a wind tunnel, bark beetles fly erratically which has discouraged more detailed studies (Choudhury and Kennedy, 1980; Salom and McLean, 1991a). In the field, bark beetles generally are recaptured downwind in the absence of attractive odors (Salom and McLean, 1991b) but this can be the result of either a directed flight downwind or a random drift with wind (Helland et al., 1984; as in the models here). Salom and McLean (1991b) found Trypodendron lineatum flew across wind to opposite sides of a clearcut valley although more were caught downwind. Bark beetles are believed to fly upwind to attractive odor sources based on direct observation and on catches of traps correlated with wind direction (references in Byers 1988; Salom and McLean, 1991b). Byers (1988) mounted wind-vanes on traps to prove that western pine beetles, Dendroctonus brevicomis, fly upwind to pheromone.

Bark beetles can accumulate within a plume at higher wind speeds and appear to fly in "groups" as in the model. On 19 May 1984 in Denmark in a clearcut about 1 km from the study site, I observed Ips typographus taking off from a brood log pile. Most flew downwind (one beetle at about 3.3 m/s over 50 m as I ran down a road parallel to its flight path) while fewer beetles flew across the wind. Nearby, I noticed several ten's of Ips typographus at the same time as they flew slowly upwind to a large fallen Norway spruce undergoing colonization. The beetles were orienting upwind presumably within a pheromone/host odor plume from at least as far as 50 m from the tree. The beetles were tossed horizontally across the wind line, or possibly were casting, as they slowly progressed upwind at a ground speed of at most 0.5 m/s (compared to my slow walking) and often were blown downwind during gusts. The wind was unidirectional but variable in speed from about 1 to 4 m/s (fan anemometer at 1.5 m for 20-30 s). Most individuals were flying from 2-4 m height (practically all < 6 m) while 15-30 m from the tree, but generally lower (1-3 m) when approaching within 10 m of the tree.

Many moths have a zigzagging flight during anemotaxis (Kennedy, 1983; Baker and Haynes, 1987) while model insects flew directly upwind with random deviations. The programmed counterturning flight could be included for more realism but should not greatly affect the relationships since the mean direction of a zigzag is still directly upwind with random deviations. In spite of the simplifications of the model, simulated insects could reliably reach the odor source using only a combination of odor-modulated anemotaxis and casting. Improvements to the model with regard to plume dimensions, orientation and flight movement parameters, and wind effects probably will not alter the basic conclusion that fluctuations in wind speed and direction modify an otherwise random arrival pattern to one that is clumped and non-random. Most reports on arrival of insects to traps can not be analyzed for random arrival patterns as done here since the sampling periods were of hours or days (e.g., Byers and Löfqvist, 1989). However, Nakamura and Kawasaki (1984) report the mean wind velocity (every 5 min.) with 1-m sampling periods of arrival of S. litura to pheromone traps over two hours - but they did not speculate about randomness of the arrivals. A chi-square analysis of the S. litura data (their Figure 1) shows that this moth exhibited a clumped arrival pattern (23 df, P = 0.03).

The simulation model is available from the author as a compiled program for IBM- compatible personal computers with VGA monitor (please send a formatted disk). The software also can be downloaded from the Internet http://www.wcrl.ars.usda.gov/cec/software.htm.

Acknowledgments--Funding for the project was obtained from the Swedish Agricultural and Forest Research Council (SJFR). I appreciate the helpful discussions and comments of my colleagues here in Alnarp and Lund concerning the model, especially the interest and encouragement of Jörgen Jönsson.


REFERENCES

BAKER, T.C. 1989. Pheromones and flight behavior, pp. 231-255, in G.J. Goldsworthy and C.H. Wheeler (eds.). Insect Flight. CRC Press Inc., Boca Raton, Florida.

BAKER, T.C., and HAYNES, K.F. 1987. Manoeuvres used by flying male oriental fruit moths to relocate a sex pheromone plume in an experimentally shifted wind-field. Physiol. Entomol. 12:263-279.

BAKER, T.C., and ROELOFS, W.L. 1981. Initiation and termination of oriental fruit moth male response to pheromone concentrations in the field. Environ. Entomol. 10:211- 218.

BAKKE, A., FRo/YEN, P., and SKATTEBo/L, L. 1977. Field response to a new pheromonal compound isolated from Ips typographus. Naturwissenschaften 64:98.

BAKKE, A., SAETHER, T., and KVAMME, T. 1983. Mass trapping of the spruce bark beetle Ips typographus. Pheromone and trap technology. Medd. Norsk Inst. Skogforsk. 38:1-35.

BOSSERT, W.H., and WILSON, E.O. 1963. The analysis of olfactory communication among animals. J. Theor. Biol. 5:443-469.

BYERS, J.A. 1983. Electronic fraction collector used for insect sampling in the photoperiod- induced diel emergence of bark beetles. Physiol. Entomol. 8:133-138.

BYERS, J.A. 1988. Upwind flight orientation to pheromone in western pine beetle tested with rotating windvane traps. J. Chem. Ecol. 14:189-212.

BYERS, J.A. 1991. Simulation of mate-finding behaviour in pine shoot beetles, Tomicus piniperda. Anim. Behav. 41:649-660.

BYERS, J.A. 1992. Dirichlet tessellation of bark beetle spatial attack points. J. Anim. Ecol. 61:759-768.

BYERS, J.A. 1993. Simulation and equation models of insect population control by pheromone-baited traps. J. Chem. Ecol. 19:1939-1956.

BYERS, J.A., and LÖFQVIST, J. 1989. Flight initiation and survival in the bark beetle Ips typographus (Coleoptera: Scolytidae) during the spring dispersal. Holarct. Ecol. 12:432-440.

BYERS, J.A., BIRGERSSON, G., LÖFQVIST, J., and BERGSTRÖM, G. 1988. Synergistic pheromones and monoterpenes enable aggregation and host recognition by a bark beetle, Pityogenes chalcographus. Naturwissenschaften 75:153-155.

BYERS, J.A., ANDERBRANT, O., and LÖFQVIST, J. 1989. Effective attraction radius: A method for comparing species attractants and determining densities of flying insects. J. Chem. Ecol. 15:749-765.

BYERS, J.A., BIRGERSSON, G., LÖFQVIST, J., APPELGREN, M., and BERGSTRÖM, G. 1990. Isolation of pheromone synergists of bark beetle, Pityogenes chalcographus, from complex insect-plant odors by fractionation and subtractive- combination bioassay. J. Chem. Ecol. 16:861- 876.

CHOUDURY, J.H., and KENNEDY, J.S. 1980. Light versus pheromone-bearing wind in the control of flight direction by bark beetles, Scolytus multistriatus. Physiol. Entomol. 5:207-214.

DAVID, C.T., KENNEDY, J.S., LUDLOW, A.R., PERRY, J.N., and WALL, C. 1982. A reappraisal of insect flight towards a distant point source of wind-borne odor. J. Chem. Ecol. 8:1207-1215.

ELKINTON, J.S. and CARDÉ, R.T. 1984. Odor dispersion, pp. 73-91, in W.J. Bell and R.T. Cardé (eds.) Chemical Ecology of Insects. Chapman and Hall, London.

ELKINTON, J.S., CARDÉ, R.T., and MASON, C.J. 1984. Evaluation of time-averaged dispersion models for estimating pheromone concentration in a deciduous forest. J. Chem. Ecol. 10:1081-1108.

FARES, Y., SHARPE, P.J.H., and MAGNUSON, C.E. 1980. Pheromone dispersion in forests. J. Theor. Biol. 84:335-359.

FRANCKE, W., HEEMANN, V., GERKEN, B., RENWICK, J.A.A., and VITÉ, J.P. 1977. 2- Ethyl-1-6-dioxaspiro[4.4]nonane, principal aggregation pheromone of Pityogenes chalcographus (L.). Naturwissenschaften 64:590-591.

HELLAND, I.S, HOFF, J.M., and ANDERBRANT, O. 1984. Attraction of bark beetles (Coleoptera: Scolytidae) to a pheromone trap: Experiment and mathematical models. J. Chem. Ecol. 10:723-752.

KENNEDY, J.S. 1939. The visual responses of flying mosquitoes. Proc. Zool. Soc. Lond. A 109:221-242

KENNEDY, J.S. 1983. Zigzagging and casting as a response to windborne odour: a review. Physiol. Entomol. 8:109-120.

LINDGREN, B.S., BORDEN, J.H., CHONG, L., FRISKIE, L.M., and ORR, D.B. 1983. Factors influencing the efficiency of pheromone baited traps for 3 species of ambrosia beetles (Coleoptera: Scolytidae). Can. Entomol. 115:303-314.

MURLIS, J., and JONES, C.D. 1981. Fine-scale structure of odour plumes in relation to insect orientation to distant pheromone and other attractant sources. Physiol. Entomol. 6:71-86.

NAKAMURA, K., and KAWASAKI, K. 1977. The active space of the Spodoptera litura (F.) sex pheromone and the pheromone component determining this space. Appl. Entomol.Zool. 12:162-177.

NAKAMURA, K., and KAWASAKI, K. 1984. Male catches of Spodoptera litura (F.) in pheromone traps under fluctuating wind velocity: Validity of the active space model. Appl. Entomol. Zool. 19:192-201.

RIPLEY, B.D. 1981. Spatial Statistics. John Wiley & Sons, New York.

SABELIS, M.W., and SCHIPPERS, P. 1984. Variable wind directions and anemotactic strategies of searching for an odour plume. Oecologia 63:225-228.

SALOM, S.M., and McLEAN, J.A. 1991a. Flight behavior of scolytid beetle in response to semiochemicals at different wind speeds. J. Chem. Ecol. 17:647-661.

SALOM, S.M., and McLEAN, J.A. 1991b. Environmental influences on dispersal of Trypodendron lineatum (Coleoptera: Scolytidae). Environ. Entomol. 20:565-576.

TILDEN, P.E., BEDARD, W.D., LINDAHL, K.Q.Jr., and WOOD, D.L. 1983. Trapping Dendroctonus brevicomis: Changes in attractant release rate, dispersion of attractant, and silhouette. J. Chem. Ecol. 9:311-321.

VON KEYSERLINGK, H.C. 1984. Close range orientation of flying Lepidoptera to pheromone sources in a laboratory wind tunnel and the field. Med. Facult. Land. Rijksuniv. Gent 49:683-689.

WORNER, S.P. 1991. Use of models in applied entomology: the need for perspective. Environ. Entomol. 20:768-773.
home page