Department of Crop Science, Swedish University of Agricultural Sciences, Alnarp, Sweden.
Present address:
Chemical Ecology

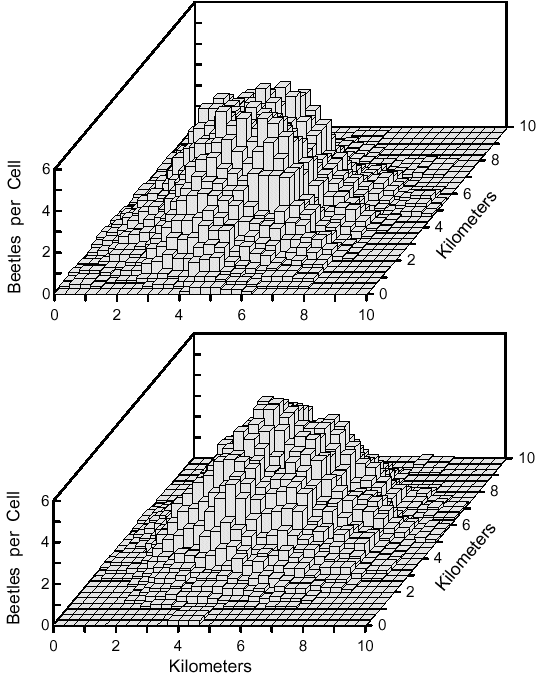
 Opening screen of software for simulation and calculation of mean dispersal distance
Opening screen of software for simulation and calculation of mean dispersal distance
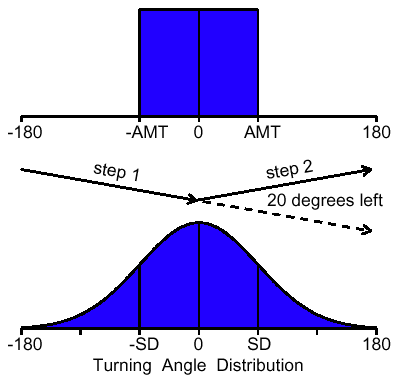
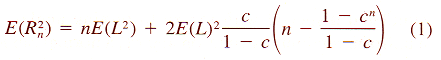
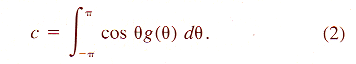
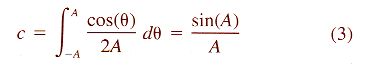
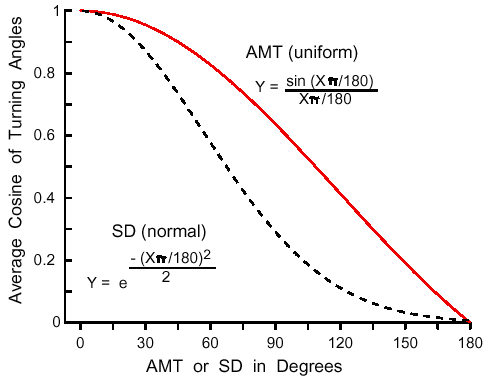
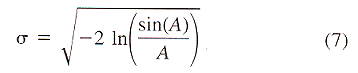
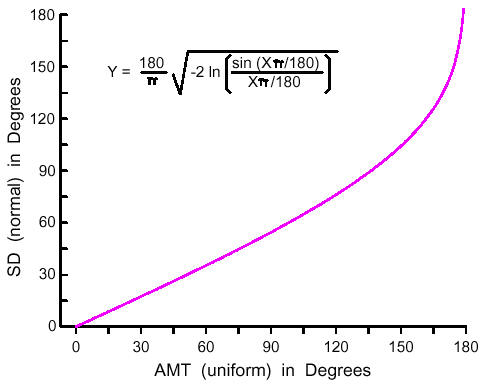
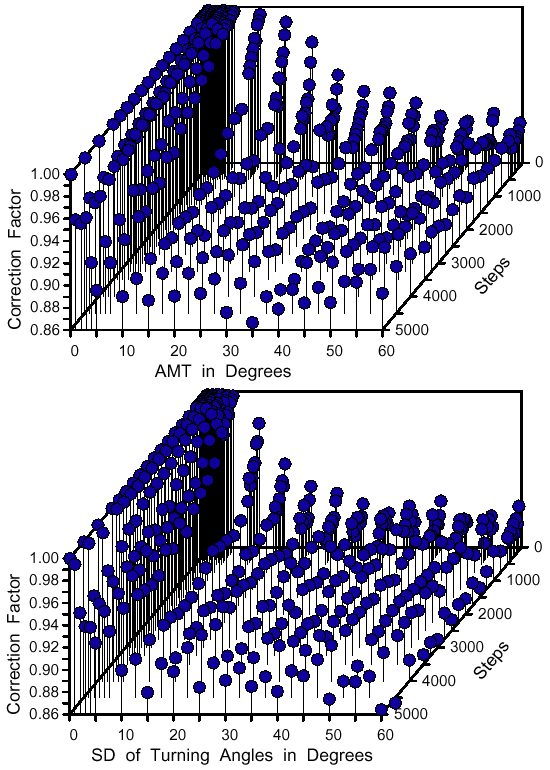
| Z = aX3 + bX2 + cX + dX2Y + eXY + fXY2 + gY + hY2 + iY3 + j | (8) |
|---|
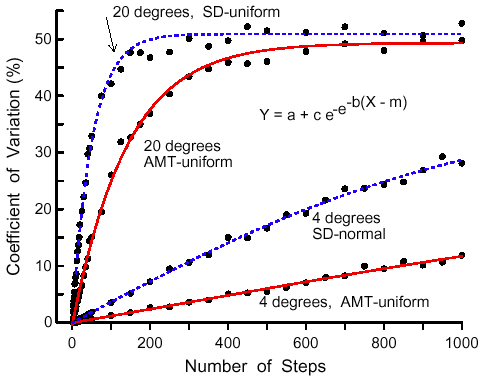
|
Table 1. Prediction of mean dispersal distance (MDD) after I000
steps for the nematode Steinernema carpocapsae and
various insects (data from literature) based on mean step
length and SDA.
| |||
| Organism (study) | meam step length (N) | SDA (°) | MDD after 1000 steps (time)a |
|---|---|---|---|
| Nematode: Steinernema carpocapsae on 1% agar (original data) | 0.3515 mm (1403) | 19.66 | 5.76 cm (4.88 h) |
| Ant: Serrastruma lujae foraging (A. Dejean in Bovet and Benhamou 1988) | 1.5 cm (664) | 46.98 | 1.03 m (67.8 min) |
| Ant: Tapinoma nigerrimum foraging (Lopez et al. 1997) | 2.68 cm (29) | 33.7 | 2.56 m (33.3 min) |
| Darkling beetle: Eleodes extricata in grass (Crist et al. 1992) | 4 cm | 53.75b | 2.42 m (83.3 min) |
| Ground beetle: Pterostichus melanarius (Wallin and Ekbom 1988) | 1.28 m (86) | 44.68c | 92.62 m (10.42 d) |
| Butterfly: Pieris rapae ovipositing (Root and Kareiva 1984) | 2.56 m (327)c | 48.06c | 172.44 m (5.56 h) |
| Butterfly: Euphydryas editha (Turchin et al. 1991) | 7.16 m (140) | 56.02b | 415.5 m |
| Weevil: Hylobius abietis on sand (Kindvall et al. 2000) | 8.72 cm (78) | 23.99d | 11.71 m (2.78 h) |
| Hymenopteran parasitoid: Pnigalio soemius (Casas 1988) | 2 mm (55) | 41.43d | 15.59 cm |
|
aBased on mean velocity bConverted from mean vector length (or mean cosine) with Eq. 11. cGenerated from histogram of turning angles or step sizes using random variates dConverted from absolute angular deviation (ADD), SDA = (ADD + 0.31)/0.8136. | |||
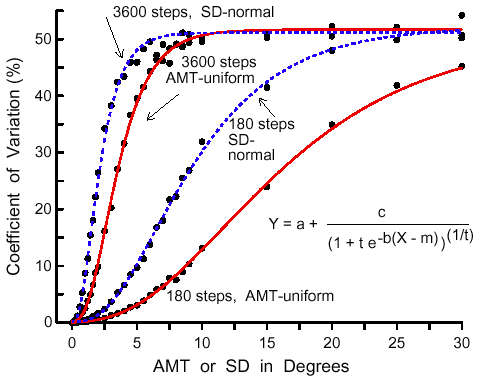
|
Table 2. Prediction of the mean dispersal distance (MDD)
based on different segmentations of a 2001 step walk (2-m steps of 30° SDA)
resulting in different numbers of steps, mean step sizes, and mean cosine of turning angles.
| |||
| Steps (divisor) | Mean step size ± 1 SD | Mean cosine ± 1 SD | MDD |
|---|---|---|---|
| 2000 (1) | 2.000 ± 0 | 0.8710 ± 0.1737 | 303 |
| 1000 (2) | 3.856 ± 0.203 | 0.8200 ± 0.2385 | 344 |
| 500 (4) | 7.328 ± 0.654 | 0.6938 ± 0.3854 | 342 |
| 333 (6) | 10.488 ± 1.278 | 0.5710 ± 0.4902 | 325 |
| 250 (8) | 13.456 ± 2.165 | 0.4589 ± 0.5519 | 310 |
| 200 (10) | 16.067 ± 3.061 | 0.3656 ± 0.5981 | 296 |
| 100 (20) | 26.242 ± 8.159 | 0.1828 ± 0.7016 | 280 |
| 40 (50) | 45.38 ± 20.17 | 0.1457 ± 0.6664 | 294 |
| 20 (100) | 71.24 ± 32.20 | 0.0973 ± 0.6852 | 311 |
| 10 (200) | 98.47 ± 63.15 | 0.0641 ± 0.7117 | 294 |
| Note: The segmentations, after the first step, were done by connecting every coordinate, or every second or more as indicated (divisor) to obtain the number of steps. | |||
|
JOHN A. BYERS
Department of Crop Science, Swedish University of Agricultural Sciences, Alnarp, Sweden. Present address: Chemical Ecology 
|
|---|